4 bit Magnitude Comparator
By gyaanibuddy_admin,
This is '4 bit Magnitude Comparator' assignment of Digital Design - Computer Engineering of Somaiya University - Gyaani Buddy
AIM: Design a 2-bit comparator using logic gates and verify 4-bit magnitude comparator using IC 7485
This is '4 bit Magnitude Comparator' assignment of Digital Design - Computer Engineering of Somaiya University - Gyaani Buddy
The comparison of two numbers is an operator that determines one number is greater than, less than (or) equal to the other number. A magnitude comparator is a combinational circuit that compares two numbers A and B and determines their relative magnitude. The outcome of the comparator is specified by three binary variables that indicate whether A>B, A=B (or) A<B.
Two Bit Magnitude Comparator Implementation Details:
Truth Table
|
A1 |
A0 |
B1 |
B0 |
A > B |
A = B |
A < B |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
||||||
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
||||||
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
11 |
||||||
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
||||||
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
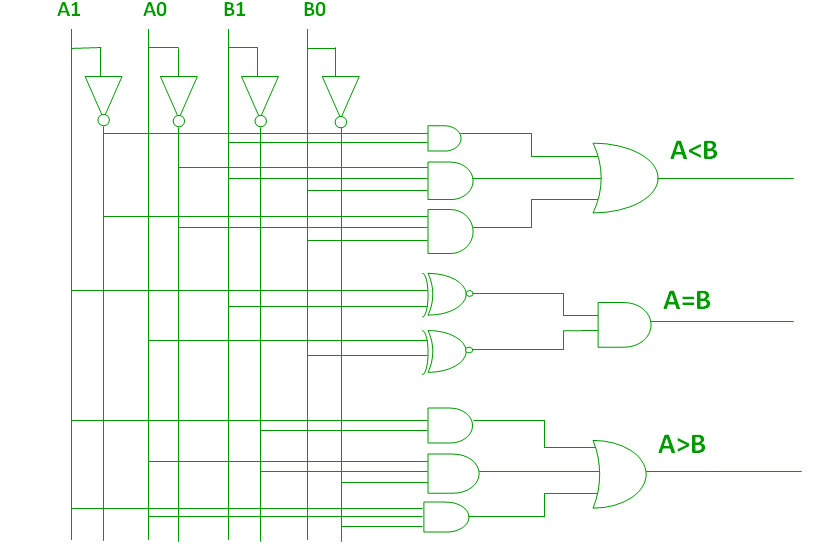
From the Truth Table:
(A<B) = A1’B1 + A0’B1B0 +A1’A0’B0
(A=B) = A1’A0’B1’B0 ’+ A1’A0 B1’B0 +A1A0B1B0 + A1A0’B1B0’
=A1’B1’ (A0’B0’ +A0B0) + A1B1 (A0B0+A0’B0’)
= (A0B0+A0’B0’) (A1B1+A1’B1’)
= (A0 EX-NOR B0) (A1 EX-NOR B1)
(A>B) = A1B1’ + A0B1’B0 ’+A1A0B0’
Logic Diagram of 2 bit Comparator
Four Bit Magnitude Comparator Implementation Details
Pin Diagram of IC 7485
Logic Diagram of IC 7485
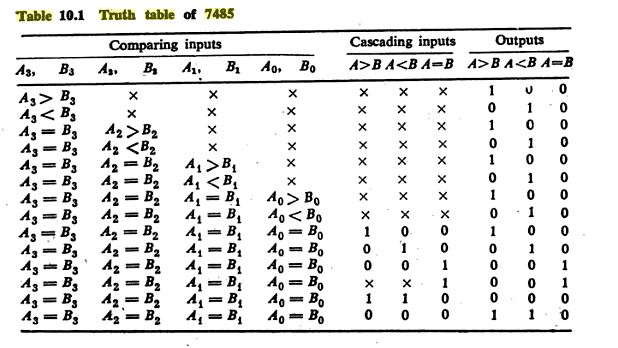
Comparing Table
1. Design a 1- bit magnitude comparator using logic gates.
Ans 1:A comparator used to compare two bits is called a single bit comparator. It consists of two inputs each for two single bit numbers and three outputs to generate less than, equal to and greater than between two binary numbers.
Truth Table:
A>B = AB’
A<B = A’B
A=B = A’B’ +AB
THUS:
(A>B) + (A<B) = A’B + AB’
NOW TAKE COMPLEMENT BOTH SIDES
((A>B) + (A<B))’ =( A’B + AB’)’
((A>B) + (A<B))’ = AB’ + A’B
((A>B) + (A<B))’ = (A+ B’) (A’ + B)
((A>B) + (A<B))’ =( AA’ +AB + A’B’ +BB’)
((A>B) + (A<B))’= (AB +AB’)
